Chapter 6 - Coherence

⊕
“But what is coherence? Given a large number of elements (propositions, concepts, or whatever) that are coherent or incoherent with each other in various ways, how can we accept some of these elements and reject others in a way that maximizes coherence? How can coherence be computed?” – Thagard & Verbeurgt (1998) In the previous chapter you practiced making a formal computational-level model of subset choice. In this chapter we study a computational-level model of coherence developed by cognitive scientists and published in the journal Cognitive Science. The pedagogical goal is to see how these scientists motivated their modeling decisions, what properties their formalization has, what limitations it has, and how it may be revised or expanded.

We have selected this particular model for our purposes because it combines simplicity with wide applicability. It also allows us to illustrate how mathematical proofs can be used to derive model properties.

Coherence as constraint satisfaction

In 1998, computational philosopher Paul Thagard and computer scientist Karsten Verbeurgt proposed a model of a wide range of phenomena that can all be seen as falling under a single banner: ‘maximizing coherence’.

Thagard and Verbeurgt wanted to explain this capacity for sense making computationally. Intuitively, they saw the computational-level problem as follows:

Coherence (informal)
Input: Networks of interconnected elementsElements can be any type of mental representations (concepts, propositions, hypotheses, images, goals, actions, plans, etc.). , where connections in the network represent coherence and incoherence relations between pairs of elements.Coherence relations include explanation, implication, positive association. Incoherence relations include inconsistency, incompatibility, and negative association.
Output: Accept and reject elements in a way that is maximally coherent.

Inspired by the notion of constraint satisfaction studied in computer science, the scientists formalized coherence and incoherence relations as positive and negative constraints, respectively. These constraints have well-defined satisfaction conditions: A positive constraint \((a,b) \in C^+\) is satisfied if and only if the elements \(a\) and \(b\) are both rejected or both accepted. A negative constraint \((a,b) \in C^-\) is satisfied if and only if the element \(a\) is accepted and \(b\) is rejected, or conversely, element \(b\) is accepted and \(a\) is rejected.

Using these definitions, the problem of maximizing coherence can be made a bit more formal, as follows:

Coherence (pre-formal)
Input: A network of elements, with pairs of elements connected by positive or negative constraints.
Output: A partition of the set of elements into sets \(A\) (accepted) and \(R\) (rejected) elements such that the number of satisfied constraints is maximized.

Using mathematical notation from the section on graph theory in Chapter 3, we can make this more precise and explicit:We deviate a bit from the notation used by the original authors and make the link to graph theory transparent.

Coherence (formal, version 1)
Input: A graph \(G = (V, E)\) with vertex set \(V\) and edge set \(E \subseteq V \times V\) that partitions into positive constraints \(C^+\) and negative constraints \(C^-\) (i.e., \(C^+ \cup C^- = E\) and \(C^+ \cap C^- = \emptyset\)).
Output: A partition of the vertices \(V\) into sets \(A\) and \(R\) such that \(Coh(A,R)=\) \(|\{(u,v)~|~(u,v) \in C^+,\) \(u,v \in A\) \(\text{ OR }\) \(u,v \in R \}|\) \(+\) \(|\{(u,v)~|~(u,v) \in C^{-},\) \(u \in A, v \in R\) \(\text{ OR }\) \(v \in A, u \in R \}|\) is maximum.\(Coh(A,R)\) is said to be maximum if there exists no alternative partition \(X,Y\) with \(Coh(X,Y) >\) \(Coh(A,R)\).

The following figure illustrates the idea.

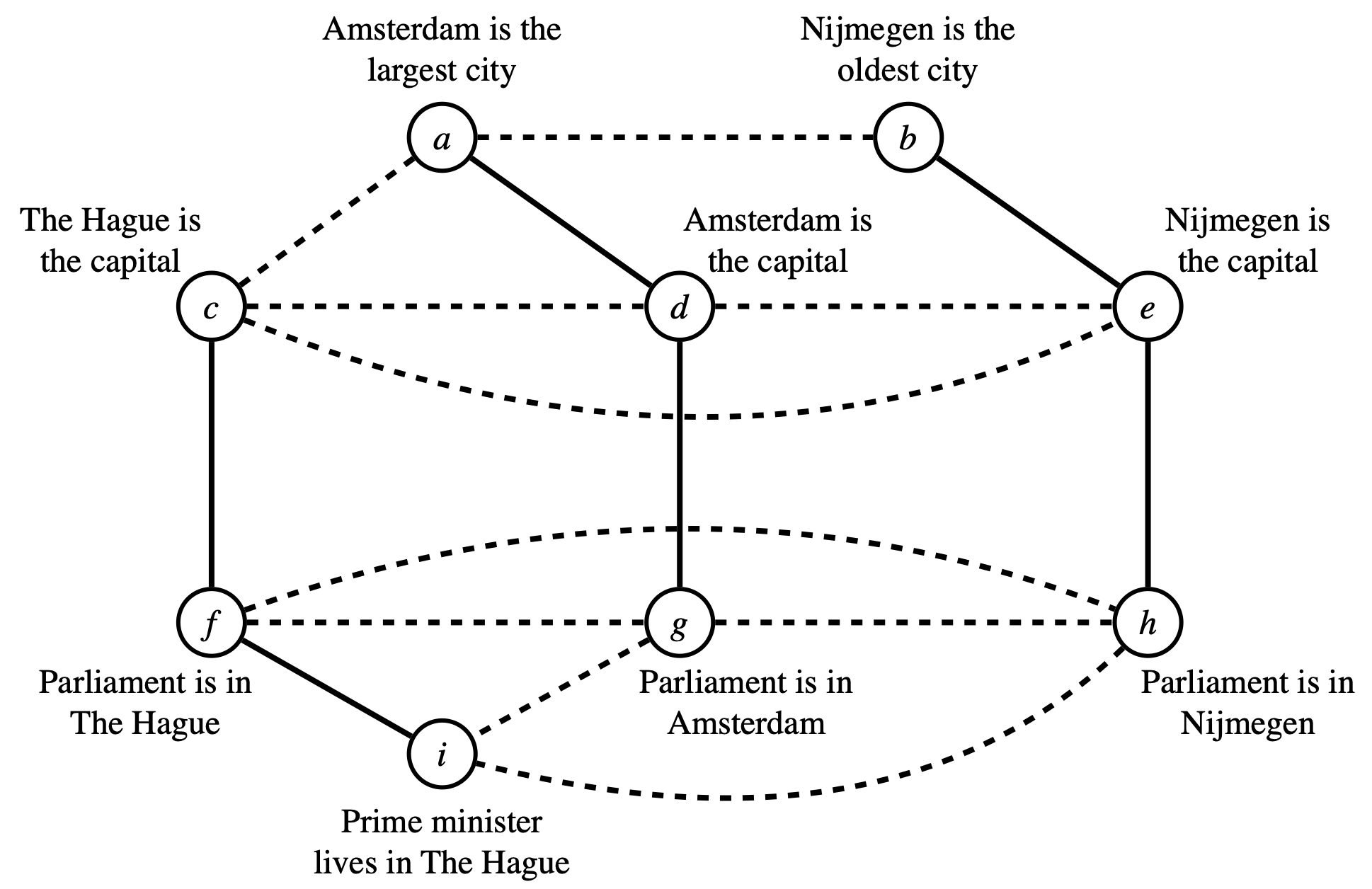
Lastly, we introduce weights on the constraints in the model. This captures Thagard and Verbeurgt’s intuition that some pairs of elements can cohere and incohere more strongly than others:

Coherence (formal, version 2)
Input: A graph \(G = (V, E)\), where \(E = C^+ \cup C^-\) (\(C^+ \cap C^- = \emptyset\)), and a weight \(w(u,v) \in \mathbb{N}\) for each edge \((u,v) \in E\).
Output: A partition of the vertices \(V\) into sets \(A\) and \(R\) such that \(Coh(A,R)= \sum_{(u,v) \in C^+, u,v \in A \text{ OR } u,v \in R} w(u,v) + \sum_{(u,v) \in C^{-}, u \in A, v \in R \text{ OR } v \in A, u \in R } w(u,v)\) is maximum.

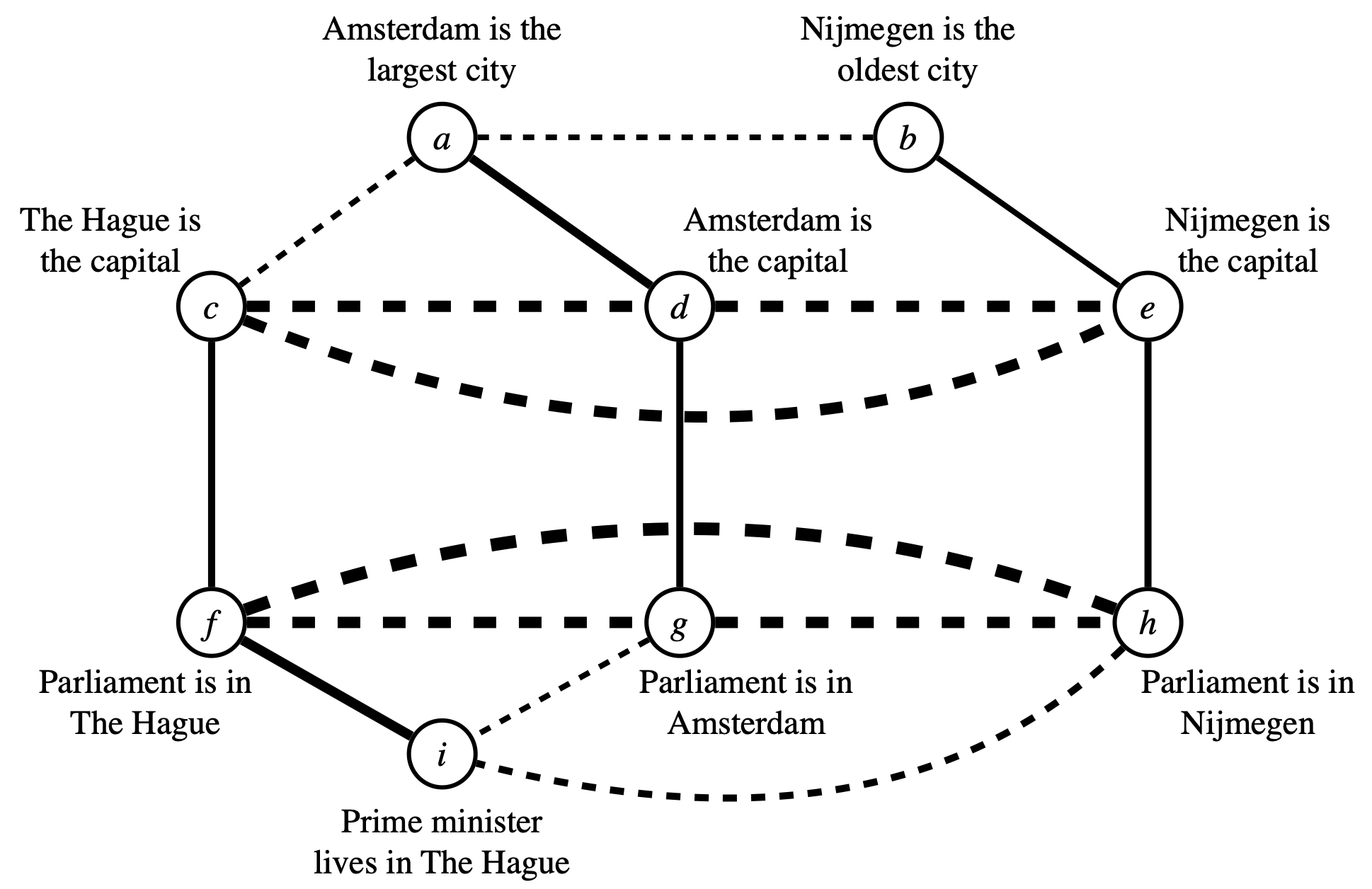
Equivalence

With version 2 of Coherence we presented one possible formal way of expressing Thagard and Verbeurgt’s ideas. We could have picked a different mathematical way of expressing the same ideas. For instance, instead of speaking of an accepted set and rejected set, we could define a function \(T\) that assigns to every vertex a truth value, i.e., \(T: V \rightarrow \{\top, \bot \}\).Recall from Chapter 3 that \(\top\) can be read as true and \(\bot\) can be read as false. We could then express the model as follows:

Coherence (formal, version 3)
Input: A graph \(G = (V, E)\), with a weight \(w(u,v) \in \mathbb{N}\) for each edge \((u,v) \in E = C^+ \cup C^- \subseteq V \times V\) (where \(C^+ \cap C^- = \emptyset\)).
Output: A truth assignment \(T: V \rightarrow \{\top, \bot \}\) such that \(Coh(T)= \sum_{T(u) = T(v)} w(u,v) + \sum_{T(u) \neq T(v)} w(u,v)\) is maximum.

Answering Question 5.2 may have been easy enough. Once you recognize that a partition into sets \(A\) and \(R\) can be conceptualized as a truth assignment with \(A = \top\) and \(R = \bot\), and you notice that then \(T(v)=T(u)\) means the same as \(u,v \in A \text{ OR } u,v \in R\), and so on, the equivalence between the two versions becomes apparent.

Now, consider the following computational-level model inspired by the connectionist modeling tradition, and answer Question 5.3:

Harmony Maximization
Input: A Hopfiel network \(G = (V, E)\), with a weight \(w(u,v) \in \mathbb{Z}\) for each edge \((u,v) \in E = V \times V\) (i.e., the network is fully connected).
Output: An activation pattern \(a: V \rightarrow \{-1,1 \}\) such that \(H(a) = \sum_{u,v \in V} a(u)a(v)w(u,v)\) is maximum.

Lessons

The exercises illustrate a few lessons. Models that look very different may not be different at all. Before considering models as explanatory competitors, it is good practice to first verify that they are not equivalent. The answer to Question 5.2 shows that even models from very different modeling traditions (e.g., symbolic versus connectionist)See e.g. Fodor & Pylyshyn (1988). can be equivalent at the computational level of explanation.

Properties

Let’s see if we can prove some properties of Coherence.

Symmetry property

Coherence has the property that \(Coh(A,R) = Coh(R,A)\) (or, equivalently, \(Coh(T) = Coh(\neg T)\)). We call this the symmetry property.

The symmetry property seems cognitively implausible when explaining how people decide what to believe as true or false (a capacity known as belief fixation). To see why, consider that the model predicts the following: If you would mentally flip all your beliefs—such that what you currently believe to be truee.g., the belief that Amsterdam is the capital of The Netherlands. you will from then on believe to be false and what you currently believe to be falsee.g., the belief that the Moon is made of cheese. you will from then on believe to be true—your new mental state will still be equally (maximally) coherent. This seems wrong!

If the symmetry property would really hold for our mental states then we would never have stable beliefs. We’d go through life flip-flopping our thoughts without anything forcing us to stabilise our beliefs. There would also be no relationship between our beliefs and the world (e.g., believing that the Moon is made of cheese would make perfect sense to all of us).

Judging from experience, it is unlikely that our minds operate this way. More likely, the model needs adjusting.

Data priority principle

The authors of the Coherence model seemed aware of the problem posed in the previous subsection. They proposed that the data priority principle counters the problem.Data priority principle: “Propositions that describe the results of observation have a degree of acceptability on their own.” – Thagard (1989) For instance, if you see the prime minister regularly arriving at the parliament building by bike, then you will believe that he cycles to work. This belief is based on direct observation, and therefore has a degree of acceptability of its own, independent of its coherence with other beliefs you may have. By maximizing coherence grounded in observations our beliefs aren’t merely circular contrivances of our minds.

Thagard and Verbeurgt proposed two different ways in which this idea could be worked out to a revised theory of coherence:

Let’s consider how these intuitive ideas can be formalized, starting with Foundational Coherence.

Foundational Coherence
Input: A graph \(G = (V, E)\), with a weight \(w(u,v) \in \mathbb{N}\) for each edge \((u,v) \in E = C^+ \cup C^- \subseteq V \times V\) (where \(C^+ \cap C^- = \emptyset\)), and special (data) elements \(D \subseteq V\).
Output: A truth assignment \(T: V \rightarrow \{\top, \bot \}\) such that \(T(d) = \top\) for each \(d \in D\) and \(Coh(T)= \sum_{T(u) = T(v)} w(u,v) + \sum_{T(u) \neq T(v)} w(u,v)\) is maximum.

The acceptability of beliefs representing direct observations (modelled by \(D\)) can impact the plausibility of other beliefs through maximizing coherence. For instance, if you already know that the parliament building is in The Hague and you observe the prime minister arriving there by bike then it is most coherent to believe that the prime minister lives in The Hague.

In Foundational Coherence, the elements of \(D\) cannot themselves be doubted. However, people are able to doubt that their observations are true if disbelieving them is more globally coherent against the background of many other beliefs. For instance, if someone told you that the prime minister lives in Amsterdam and you know that the parliament building is in The Hague and you notice that every time the prime minister arrives by bicycle there was is a camera crew and journalists waiting to interview him, then you may no longer believe he is cycling to work from his home. A more coherent interpretation may be that he wants to give a public impression to Dutch voters that he is the kind of person who cycles to work.

We can capture this idea in an adjusted formalization of Coherence called Discriminating Coherence.

Discriminating Coherence
Input: A graph \(G = (V, E)\), with a weight \(w(u,v) \in \mathbb{N}\) for each edge \((u,v) \in E = C^+ \cup C^- \subseteq V \times V\) (where \(C^+ \cap C^- = \emptyset\)), and special (data) elements \(D \subseteq V\) with a weight \(w(d) \in \mathbb{N}\) for each \(d \in D\).
Output: A truth assignment \(T: V \rightarrow \{\top, \bot \}\) such that \(Coh(T)= \sum_{d \in D, T(d) = \top} w(d) + \sum_{T(u) = T(v)} w(u,v) + \sum_{T(u) \neq T(v)} w(u,v)\) is maximum.

It seems inutuitive that, to the extent that beliefs corresponding to direct observations are truthful or accurate, the beliefs that cohere with them are also more likely to be true. Thagard and Verbeurgt indeed assumed this to be the case. Perform the next exercises to assess whether or not the intuition is founded.

NP-hard

Thagard & Verbeurgt proved another interesting mathematical property of their model, i.e., it is NP-hard. You may not yet be familiar with this term. But no worries! We have your back.

Explaining NP-hardness in great depth is beyond the scope of this bookWe wrote a different textbook on the topic. Chapter 1 is a good place to start. , but luckily it is also not necessary. For present purposes it suffices to understand that NP-hard means really quite hard. So hard in fact that such problems are also called intractable. Why? Well, if a problem is NP-hard then there cannot exist any efficient (read: polynomial-timeAn algorithm is said to run in polynomial time if the number of steps it takes can be upperbounded by a function of the form \(n^c\), where \(c\) is some constant and \(n\) is the input size. For instance, \(n^2\) is a polynomial, and so is \(n\) and \(n^3\). But e.g. \(2^n\) is exponential, and not polynomial. ) algorithm that computes the problem.Unless P = NP. For an explanation watch this video. Such problems may be computable in, say, exponential time. But exponential time grows astronomically fast as the input size grows. So fast, in fact, that even for intermediate size inputs the computation time is prohibitive.

You may want to compare the number that you obtained to the number of seconds that have past since the Big Bang, i.e., \(10^{27} < 2^{100}\) seconds. Now you understand why exponential time is prohibitively long. The type of cognitive capacity that Coherence is intended to explain runs on a time scale of seconds or minutes, or in rare cases, hours, days or weeks, but certainly not on a time scale of eons. The property ‘NP-hard’ is thus a model property that poses a serious challenge for cognitive scientists: How could a computational-level model explain (or even describe) a cognitive capacity if the postulated input-output mapping cannot be realized by any algorithm in a reasonable time?

Computing coherence

Thagard and Verbeurgt were not so easily swayed by the NP-hard property. They proposed not one, not two, but even five algorithms for computing Coherence.

We will consider some of these algorithms more in depth in Chapter 11. For now, it is important to realize that only one of the algorithms is guaranteed to return the maximum coherence truth assignment for any given instance of Coherence.

Four of the five algorithms proposed are at best heuristics. That is, they do not guarantee that they compute Coherence correctly. Even the fifth algorithm which makes a kind of guarantee makes no guarantees on how much that truth assignment that it returns resembles the maximum coherent truth assignment. In fact, a truth assignment with close to maximum coherence can be arbitrarily different from the maximum coherence truth assignment.See van Rooij & Wareham (2012). Given that Coherence is NP-hard there cannot exist any tractable algorithm that approximates the problem in the latter sense.

We will return to this topic in Chapter 11. There we will explore how well or poorly different algorithms approximate Coherence, Foundational Coherence and Discriminating Coherence, and the implications thereof.

Further reading

In this chapter we revisited the genesis of a classic model in the cognitive science literature and some of its formal properties.

Since its conception, the constraint satisfaction model of coherence has proven applicable in a large variety of contexts. For instance, it has been used to model how people may change beliefs about climate change (Thagard & Findlay, 2010), how doctors explain disease (Thagard 2018), how people fix miscommunications (van Arkel, 2021), how scientists form explanations of natural phenomena (Thagard, 2000; 2007; see also Maier, van Dongen & Borsboom, 2021), and a whole host of other situations (Thagard, 2000).

In his book Hot Thought, Paul Thagard (2008) showed how the modeling principles could be extended to include even emotions, not just beliefs and mental representations. This idea led to new accounts of how emotional coherence plays a role in religious beliefs (Thagard, 2005), how juries make guilty versus innocent verdicts (Thagard, 2003), and the formation of social attitudes (Thagard, 2008; see also Klapper et al., 2018). Most recently, Thagard (2021) also applied the model to account for people’s beliefs about COVID.

The coherence model also has its critics.Maybe you have your own criticisms? Then we invite you to articulate them and write down your arguments as precisely and rigorously as possible. For instance, Millgram (2003) critiqued the model for mixing up ‘maximizing coherence’ with ‘approximating truth’ (but see also the response by Thagard, 2012). Millgram’s critique furthermore inspired work on different notions of approximation (van Rooij & Wareham, 2012). These distinctions will prove relevant in Chapter 11.

References

van Arkel, J. (2021). How do people resolve misunderstanding in conversation through repair? Introducing a framework built on belief revision and coherence. MSc thesis, University of Groningen.

Klapper, A., Dotsch, R., van Rooij, I., & Wigboldus, D. H. (2018). Social categorization in connectionist models: A conceptual integration. Social Cognition, 36(2), 221-246.

Maier, M., van Dongen, N., & Borsboom, D. (2021). Comparing Theories with the Ising Model of Explanatory Coherence. PsyArXiv.

Millgram, E. (2000). Coherence: The price of the ticket. The Journal of Philosophy, 97(2), 82-93.

Thagard, P. (1989). Explanatory coherence. Behavioral and brain sciences, 12(3), 435-467.

Thagard, P. (2000). Coherence in thought and action. MIT press.

Thagard, P. (2003). Why wasn’t OJ convicted? Emotional coherence in legal inference. Cognition and emotion, 17(3), 361-383.

Thagard, P. (2005). The emotional coherence of religion. Journal of Cognition and Culture, 5(1-2), 58-74.

Thagard, P. (2007). Coherence, truth, and the development of scientific knowledge. Philosophy of science, 74(1), 28-47.

Thagard, P. (2008). Hot thought: Mechanisms and applications of emotional cognition. MIT press.

Thagard, P. (2012). Coherence: The price is right. The Southern Journal of Philosophy, 50(1), 42-49.

Thagard, P. (2018). Social equality: Cognitive modeling based on emotional coherence explains attitude change. Policy Insights from the Behavioral and Brain Sciences, 5(2), 247-256.

Thagard, P. (2018). How scientists explain disease. Princeton University Press.

Thagard, P. (2021). The cognitive science of COVID-19: Acceptance, denial, and belief change. Methods.

Thagard, P., & Findlay, S. (2010). Changing minds about climate change: Belief revision, coherence, and emotion. In Belief revision meets philosophy of science (pp. 329-345). Springer, Dordrecht.

Thagard, P., & Verbeurgt, K. (1998). Coherence as constraint satisfaction. Cognitive Science, 22(1), 1-24.

van Rooij, I., & Wareham, T. (2012). Intractability and approximation of optimization theories of cognition. Journal of Mathematical Psychology, 56(4), 232-247.